Fibonacci, Parte 2: A Proporção Áurea

Na primeira parte da série falei sobre a Sequência de Fibonacci e o problema da população de coelhos. Agora falarei sobre a Proporção Áurea, que está diretamente relacionada aos números descritos anteriormente.

Fibonacci, Parte 1: A sequência de Fibonacci e os coelhos.
Fibonacci, Parte 2: A Proporção Áurea.
Fibonacci, Parte 3 (final): Programação, o universo e tudo mais.

A Proporção Áurea

Como observado por Johannes Kepler (mais um do legislativo), a divisão entre um elemento da sequência de Fibonacci e seu antecessor tende a se aproximar da Proporção Áurea ( $\varphi$ ). Assim como 8 está para 5, 13 está para 8, 21 está para 13 e $F(n+1)$ está para $F(n)$ . Por exemplo: utilizando o 42° elemento, a divisão seria: $\frac{F(41)}{F(40)}$ . Porém, a Proporção Áurea pode ser calculada algebricamente, como explicarei abaixo.

Como é calculada?

Algebricamente, calculamos a Proporção Áurea tomando como base duas medidas: a e b. Utilizando dois segmentos de retas, podemos obter a seguinte imagem:

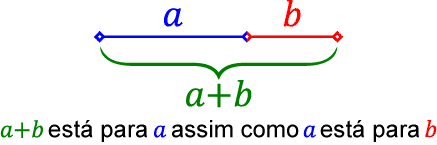
As razões $\frac{a+b}{a}$ e $\frac{a}{b}$ são iguais e constantes, e chamamos esse valor de Proporção Áurea (símbolo: $\varphi$ ). A equação obtida é:

(1) $\begin{equation*} \frac{a+b}{a} = \frac{a}{b} = \varphi \end{equation*}$

Para encontramos o valor de $\varphi$ , devemos simplificar a primeira parte da equação: $\frac{a+b}{a}=\frac{a}{a}+\frac{b}{a}=1+\frac{b}{a}}$ . Além disso, a partir da equação 1, temos: $\frac{b}{a}=\frac{1}{\varphi}$ (o inverso). Substituindo os novos valores em 1, obtemos:

(2) $\begin{equation*} 1+\frac{1}{\varphi} = \varphi \end{equation*}$

Podemos simplificá-la ainda mais: igualando os denominadores (multiplicando todos os itens por $\varphi$ ), obtendo $\varphi+1=\varphi^2$ . Podemos organizá-la passando $\varphi^2$ para o lado esquerdo (ou “adicionando $-\varphi^2$ aos dois lados da equação”) e multiplicando toda a equação por $-1$ , obtendo uma equação quadrática (de Segundo Grau):

(3) $\begin{equation*} \varphi^2-\varphi-1=0 \end{equation*}$

Para obtermos o valor de $\varphi$ basta apenas usar a queridíssima Fórmula de Bhaskara, utilizando os valores $a=1$ , $b=-1$ e $c=-1$ :

$\varphi = \frac{-b \pm \sqrt{b^2-4ac}}{2a}\$

$\varphi = \frac{-(-1) \pm \sqrt{(-1)^2-4\cdot{1}\cdot{(-1)}}}{2\cdot{1}}\$

$\varphi = \frac{1 \pm \sqrt{1+4}}{2}\$

$\varphi = \frac{1 \pm \sqrt{5}}{2}\$

Como só nos interessa o valor positivo – você não vai querer ter uma medida negativa, vai? –, o resultado é:

(4) $\begin{equation*} \varphi = \frac{1+\sqrt{5}}{2}\, \approx 1.618033988749895 \end{equation*}$

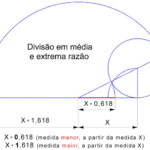
O valor colocado acima é exatamente o arredondamento utilizando o tipo float em programação: $1.618033988749895$ . Agora você está pronto para utilizá-la! Se você quer uma medida maior, basta multiplicar por $\approx 1.618$ , se quiser uma menor, por $\approx 0.618$ , como mostrado na imagem a seguir:

Utilizando X = 10, a medida menor seria 6,18 e a maior seria 16,18. (Adaptado de Wikimedia Commons)

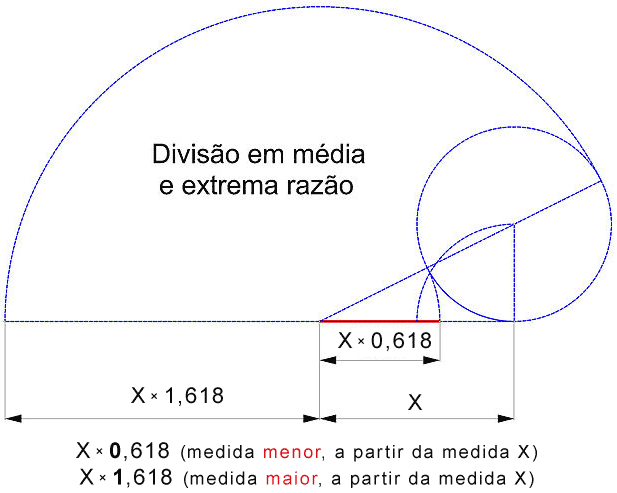
Onde podemos vê-la?

Os números de Fibonacci na Natureza — você também pode ver ~~com pão~~ em HD

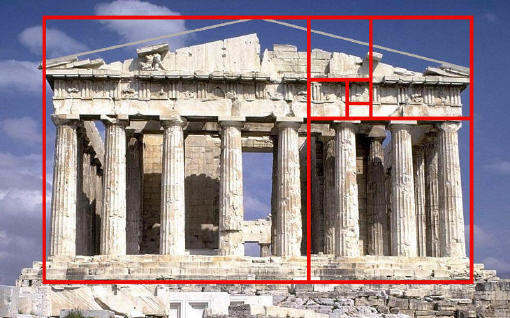
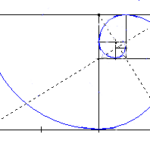
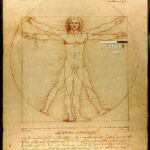
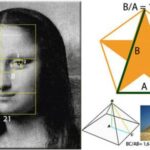
Como visto no vídeo acima, a proporção áurea pode ser encontrada em diversos locais na natureza, como em plantas, caracóis (espirais), abacaxis e corpo humano. A seguir, apresento uma galeria de imagens nas quais podemos ver a proporção áurea e os números de Fibonacci em ação. Divirta-se! 🙂

: Proporção áurea no Partenon de Atenas.
Fonte: http://britton.disted.camosun.bc.ca/goldslide/jbgoldslide.htm

: O Partenon, de Atenas.
Fonte: Wikimedia Commons.

: A proporção áurea em um retângulo.
Fonte: Wikimedia Commons.

: O Homem Vitruviano, de Leonardo da Vinci. As medidas dos membros corporais foram estabelecidas utilizando a proporção áurea.
Adaptado de Wikimedia Commons.

: Utilizando X = 10, a medida menor seria 6,18 e a maior seria 16,18. (Adaptado de Wikimedia Commons)

: Fonte: http://blog.miraiespana.com/en/proporcion-aurea-diseno-webs-hoteles/

: 8, 13, 21 e 34 são números da sequência de Fibonacci.
Fonte: http://newtoneamaca.blogspot.com

: O design do novo (velho) Twitter foi feito com base na Proporção Áurea.
Fonte: http://mashable.com/

A Proporção Áurea no Web Design

Como mostrado na galeria acima, o Twitter fez uso da Proporção Áurea para o design de sua página. Como em qualquer outra arte visual, no Web Design também é possível fazer uso dela, utilizando o mesmo princípio de divisão em média e extrema razão. Caso esteja interessado, dê uma olhada nesses dois artigos:

Na terceira parte desta série darei detalhes de como gerar você mesmo a sequência de Fibonacci e a proporção áurea com Javascript, dando detalhes sobre alguns tipos de algaritmos. Além disso, encontrei algo interessante (ou não) sobre o número 42.

~~Então, não entre em pânico e aguarde a próxima parte! Você pode acompanhar pelo Twitter, Facebook ou pelo RSS.~~

Atualização: Não sei se a terceira parte irá sair, talvez um dia. Se eu conseguir um tempo extra e paciência, eu posto. 😉

Atualização 2 (20/06/2014): Mais de dois anos depois e ainda não sei se terá terceira parte. Pelo jeito não. A esperança é a última que morre!

Blog do Wesley Cota

Fibonacci, Parte 2: A Proporção Áurea